首先，Tries不是一种Abstract Data Type, 而是一种specific implementation for set and map, 通常被用于储存类型是String的数据。

Case: Try to figure out a way to make it clear that our set contains “sam”, “sad”, “sap”, “same”, “a”, and “awls”.

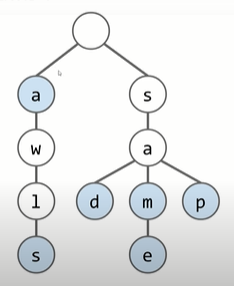
储存时将string的最后一个字符标记为蓝色。这样写contains method时，就能以该node是不是蓝色来判定单个string结束的位置。

Searching will only fail if we hit an unmarked node or we fall off the tree.

---

如果想用Tries写key为string的map时该怎么做？

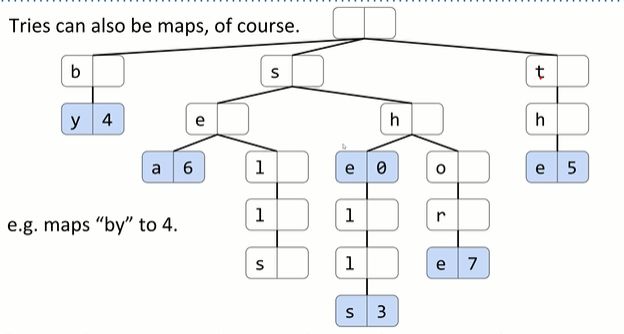
写private node class的时候，给再加一个private int value就好。

---

TriesSet 的实现：

public class TrieSet {
  private static final int R = 128; // ASCII

  private Node root;    // root of trie


  private static class Node {
    private char ch;  
    private boolean isKey;   
    private DataIndexedCharMap next;

    private Node(char c, boolean blue, int R) {
      ch = c; 
      isKey = blue;
      next = new DataIndexedCharMap<Node>(R);
    }
  }
}

Node class的结构：

每个node有：private char ch（这个node的key），private boolean isKey（这个node是不是蓝色），private DataIndexedCharMap next（长度为128的map，因为ASCII中字符有128个，每个字符对应一个map的位置，每个位置储存的是ch为该字符的node）

---

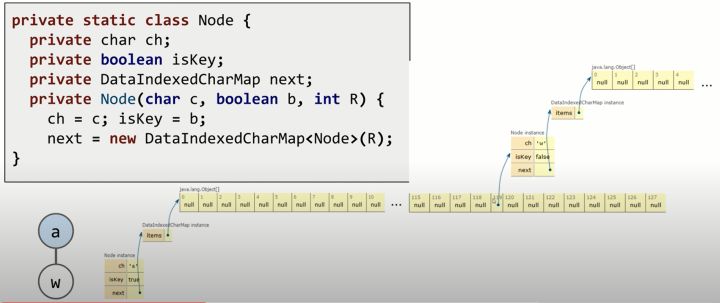
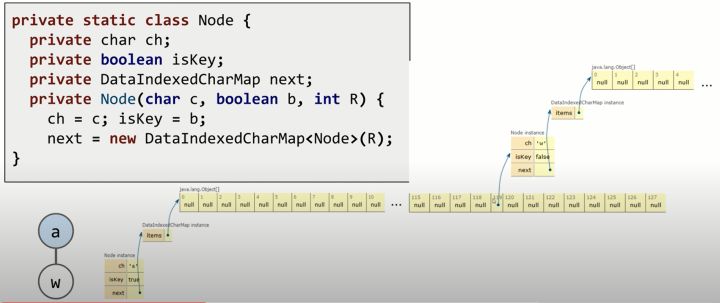
到这里，离谱的事情发生了。将node class中的private char ch 和 char c删除，一样能运行。为什么呢？因为每个node都有一个长度为128的完整的map。 当我们新增string时，按顺序根据每个char的ASCII，在node中的map里寻找对应的位置，新增node或者给node改颜色，就可以实现add功能。查找也是相同原理。 add和contains的复杂度和Tries里有多少node、多少string都没关系，只和插入和查找String的长度本身有关，所以最差情况下复杂度是 Θ(1)。

 
public class TrieSet {
  private static final int R = 128; // ASCII

  private Node root;    // root of trie


  private static class Node {
    private boolean isKey;   
    private DataIndexedCharMap next;

    private Node(boolean blue, int R) {
        isKey = blue;
        next = new DataIndexedCharMap<Node>(R);
    }
  }
}

---

问题又来了！这么做对内存很不友好，每添加一个node，需要附加新增一个长度为128的map，而且map中的大部分value都是null。

解决方法可以是将长度为128的map替换为hash table或者Balanced Binary search tree。

举例：储存”ad”，”c”

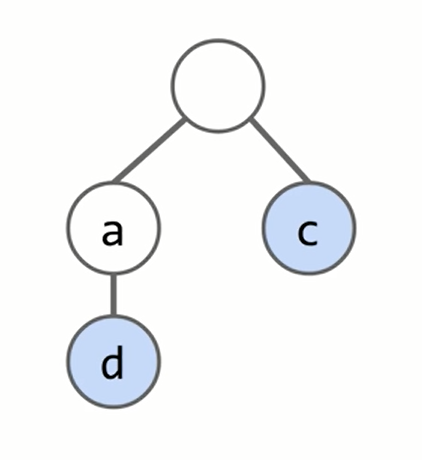
如果使用之前的map，是这样的：

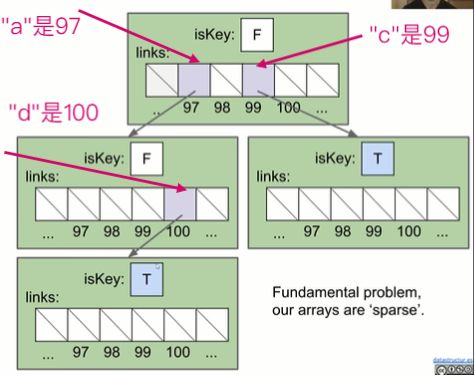
改成Buckets长度为4的hash table后：

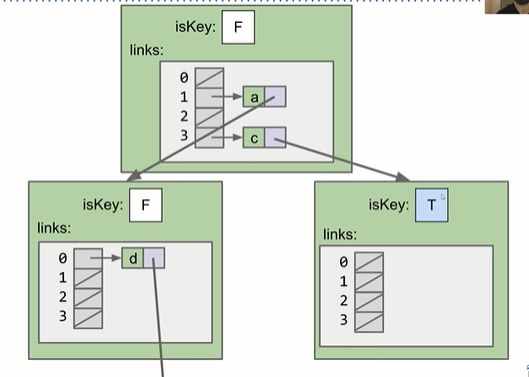
改为Balanced Binary Search Tree后：

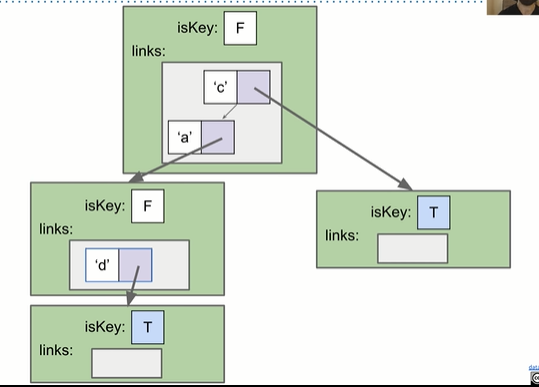
三种情况的对比：

1. DataIndexedCharMap:
   • Very fast, but memory hungry.
   • Space: 128 links per node.
   • Runtime: Θ(1)
2. Balanced BST:
   • A little slower than Hash Table, uses similar amount of memory?
   • Space: C links per node, where C is the number of children.
   • Runtime: O(log R), where R is size of alphabet.
3. Hash Table:
   • Almost as fast, uses less memory.
   • Space: C links per node, where C is the number of children
   • Runtime: O(R), where R is the size of the alphabet

Note:

• Cost per link is higher in BST and Hash Tables;
• R is a fixed number (this means we can think of the runtimes as constant).

---